프로젝트 오일러 86

내 이 세상 도처에서 쉴 곳을 찾아보았으나, 마침내 찾아낸, 컴퓨터가 있는 구석방보다 나은 곳은 없더라.

on Project-Euler Clojure

프로젝트 오일러 86

육면체의 한쪽 구석에서 다른 구석으로 가는 최단 경로 찾기

문제 자세히 보기: [국어] [영어]

직육면체를 펼쳐 평면으로 생각하면 문제를 푸는 데 도움이 된다. 평면 위의 한 점에서 다른 점으로 가는 최단 경로는 직선이다. 한쪽 구석 S 에서 다른 구석 F 로 가는 경로는 네 가지가 있다.

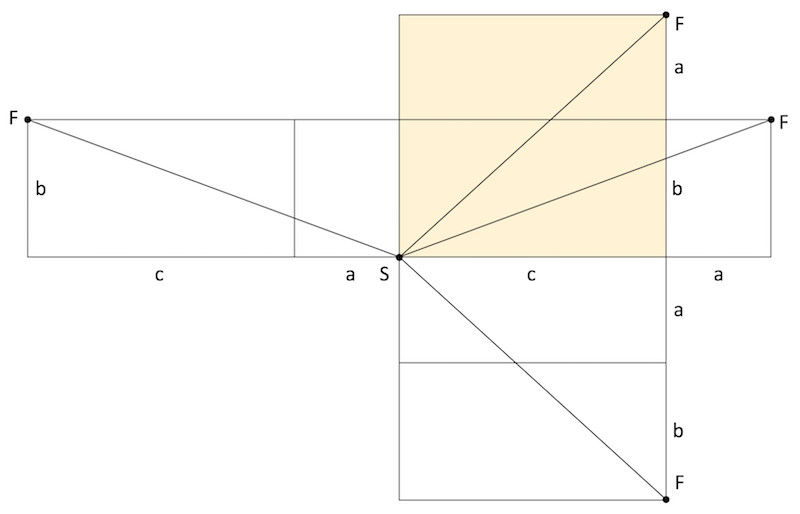
Cubic

직육면체 각 변의 길이를 a, b, c 라 하고, a \le b \le c 인 경우, 최단 경로의 길이는 다음과 같이 구할 수 있다.

%math \begin{aligned} d = \sqrt{(a + b)^2 + c^2} \end{aligned}

c = M 인 경우 a, b 를 바꿔가며 정수 해를 찾을 수 있는데, a 와 b 를 따로 바꿔가며 계산하면 계산 회수가 늘어나 답을 구하는 속도가 느려질 것이다. 각 변의 길이는 정수이고 각 변이 정수로 된 가장 작은 직각 삼각형의 변 길이는 (3, 4, 5) 이므로, 3 \le a+b \le 2M 인 경우의 조합을 찾는 게 더 빠를 것이다.

a + b \equiv l 이라 하면, c 가 정해졌을 때 3 \le l \le 2c 인 직육면체 중 최단경로가 정수인 경우의 수를 다음과 같이 구할 수 있다. l \le c 인 경우에는 a 를 1부터 \lfloor \frac{l}{2} \rfloor 까지 바꿀 수 있다. l > c 인 경우에는 a 를 \lceil \frac{l}{2} \rceil 부터 c 까지만 바꿀 수 있다.

%math \begin{aligned} count = \begin{cases} \lfloor \frac{l}{2} \rfloor & \mbox{if } l \le c, \newline c - \lfloor \frac{l-1}{2} \rfloor & \mbox{if } l > c \end{cases} \end{aligned}

Clojure 코드로는 다음과 작성할 수 있다.

(ns p086
  (:require [util :refer [perfect-square?]]))

(defn cnt [c]
  (apply +
         (for [l (range 3 (inc (* 2 c))) ; l <= a+b
               :when (perfect-square? (+ (* c c) (* l l)))]
           (if (<= l c)
             (quot l 2)
             (- c (quot (- l 1) 2))))))

이제 c 를 3부터 차례로 증가시키면서 직육면체의 개수가 1백만을 넘을 때까지 직육면체의 개수를 누적해가면 된다.

(def ^:private threshold 1000000)

(defn solve []
  (->> (iterate inc 3)
       (map (fn [x] [x (cnt x)]))
       (reductions (fn [[a1 a2] [b1 b2]] [b1 (+ a2 b2)]))
       (drop-while (fn [[M cnt]] (<= cnt threshold)))
       ffirst))

실행 결과는 다음과 같다.

p086=> (time (solve))
"Elapsed time: 197.473803 msecs"
1??8

참고